Trong bài này chúng ta cùng tìm hiểu các thuật toán tìm kiếm và triển khai các thuật toán đó với ngôn ngữ C. Thuật toán tìm kiếm là một thuật toán khá thông dụng trong nền khoa học máy tính ngày nay. Cùng mình tìm hiểu nhé!
Bài này nằm trong seri Học lập trình C từ A tới Z
Tại sao chúng ta cần thuật toán tìm kiếm
Trong hầu hết các hệ thống tin học, khi khai thác, xử lý dữ liệu chúng ta đều phải thực hiện thao tác tìm kiếm và xử lý thông tin. Chẳng hạn trong hệ thống tra cứu điểm thi, việc tra cứu, tìm kiếm kết quả thi của thí sinh diễn ra rất nhanh chóng và chính xác.
Thí sinh chỉ cần truy cập vào hệ thống tra cứu điểm thi, rồi nhập thông tin của mình như họ tên, ngày tháng năm sinh hoặc số báo danh là hệ thống nhanh chóng đưa ra kết quả thi của thí sinh đó mà không cần tìm đến trường mình dự thi để tìm hiểu kết quả thi của mình. Đây là một trong rất nhiều ứng dụng của bài toán tìm kiếm trong các hệ thống tin học.
Trong bài này, chúng ta sẽ đi tìm hiểu về bài toán tìm kiếm và nghiên cứu đánh giá các thuật giải tìm kiếm để đưa ra được giải thuật phù hợp nhất với yêu cầu của bài toán đặt ra. Tìm kiếm luôn là thao tác nền móng cho rất nhiều tác vụ tính toán.
Tìm kiếm nghĩa là tìm một hay nhiều mẩu thông tin đã được lưu trữ. Thông thường, thông tin được chia thành các mẩu tin (record), mỗi mẩu tin đều có một khóa (key) dùng cho việc tìm kiếm. Ta sẽ luôn có một khoá cho trước giống như khoá của các mẩu tin mà ta cần tìm. Mỗi mẩu tin được tìm thấy sẽ chứa toàn bộ thông tin để cung cấp cho một quá trình xử lý nào đó.
Trong bài học này, chúng ta sẽ thảo luận các thuật toán tìm kiếm:
- Thuật toán tìm kiếm nhị phân (Binary Search)
- Thuật toán tìm kiếm tuyến tính (Linear Search)
- Thuật toán tìm kiếm nội suy (Interpolation Search)
- Thuật toán tìm kiếm nhảy (Jump Search)
Thuật toán tìm kiếm nhị phân (Binary Search)
Khái niệm
Tìm kiếm nhị phân hay Binary Search là một thuật toán tìm kiếm để tìm ra vị trí của một phần tử trong một mảng được sắp xếp. Trong cách tiếp cận này, phần tử luôn được tìm kiếm ở giữa một phần của mảng.
Tìm kiếm nhị phân chỉ có thể được thực hiện trên một danh sách các phần tử đã được sắp xếp. Nếu các phần tử chưa được sắp xếp, chúng ta cần sắp xếp chúng trước khi thực hiện quá trình tìm kiếm phần tử.
Ý tưởng của thuật toán tìm kiếm nhị phân
Chú ý: Trong bài viết tôi giả sử mảng đang sắp xếp tăng dần. Với trường hợp mảng sắp xếp giảm dần, bạn đọc sau khi hiểu thuật toán sẽ có thể tự làm.
Do tính chất mảng đã sắp xếp, công việc tìm kiếm phần tử x có thể triển khai như sau:
- Xét đoạn mảng arr[left…right] cần tìm kiếm phần tử x. Ta so sánh x với phần tử ở vị trí giữa của mảng(mid = (left + right)/2). Nếu:
- Nếu phần tử arr[mid] = x. Kết luận và thoát chương trình.
- Nếu arr[mid] < x. Chỉ thực hiện tìm kiếm trên đoạn arr[mid+1…right].
- Nếu arr[mid] > x. Chỉ thực hiện tìm kiếm trên đoạn arr[left…mid-1].
Hình ảnh dưới đây mô phỏng quá trình thực hiện của thuật toán tìm kiếm nhị phân và so sánh với thuật toán tìm kiếm tuyến tính.
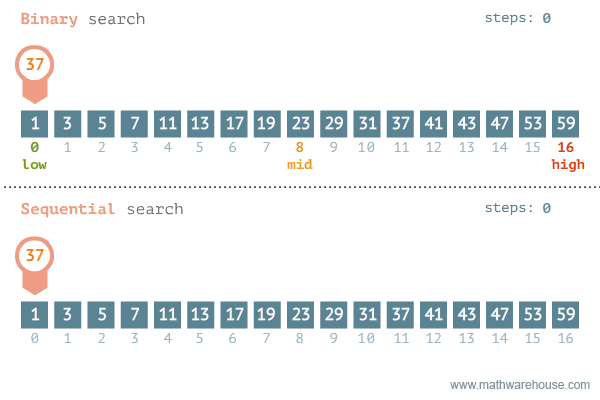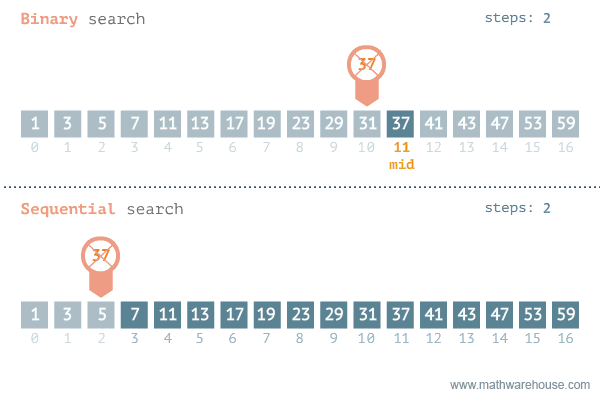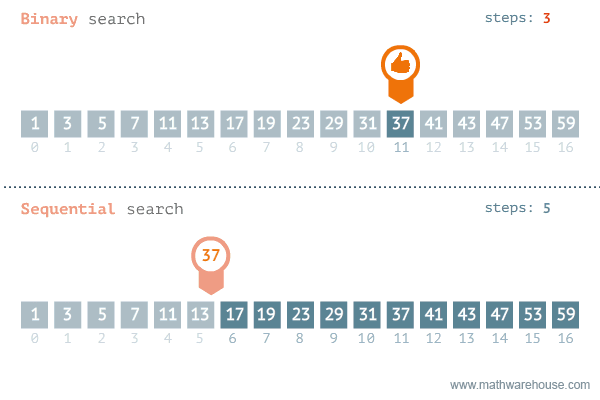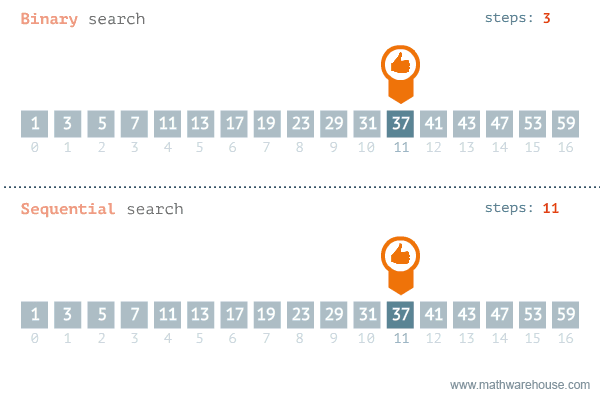So sánh thuật toán tìm kiếm nhị phân và tìm kiếm tuyến tính
Bằng cách áp dụng thuật toán tìm kiếm nhị phân, độ phức tạp cho trường hợp xấu nhất là O(log(n)).
Cách thức hoạt động của tìm kiếm nhị phân
Thuật toán tìm kiếm nhị phân có thể được thực hiện theo hai cách được thảo luận dưới đây.
- Phương pháp sử dụng vòng lặp.
- Phương pháp đệ quy.
Các bước chung cho cả hai phương pháp.
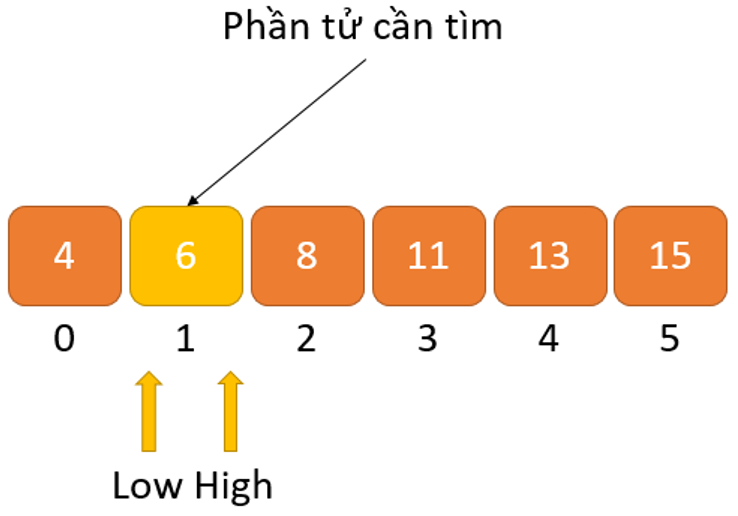
Bước 1: Giả sử ta có mảng chứa phần tử cần tìm có dạng như sau:
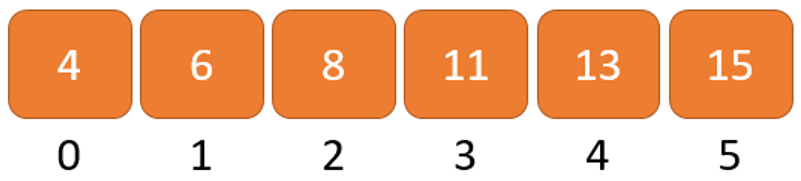
Gọi x = 6 là phần tử cần tìm.
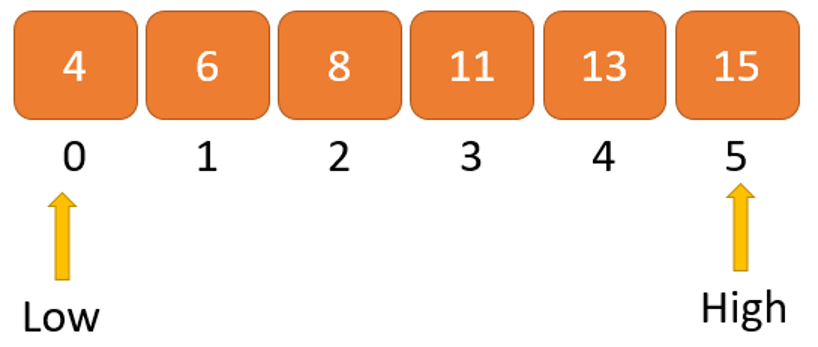
Bước 2: Đặt hai con trỏ Low và High lần lượt ở các vị trí thấp nhất và cao nhất
Bước 3: Tìm phần tử giữa ở giữa của mảng tức là (arr[(high + low)/2]) = 8
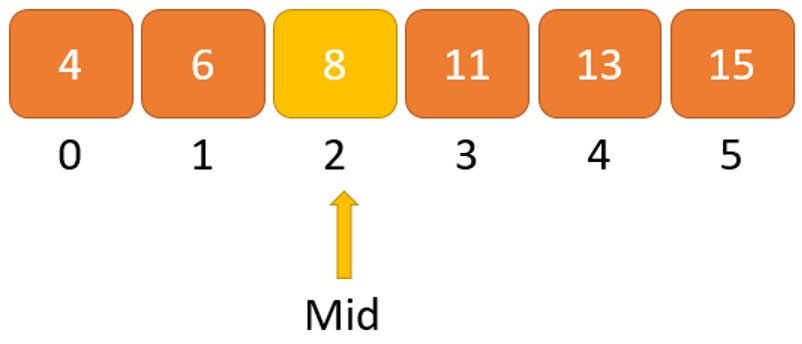
Bước 4: Nếu x == mid thì trả về mid. Nếu không thì, so sánh phần tử cần tìm với m.
Bước 5: Nếu x > mid, ta sẽ so sánh x với phần tử ở giữa của các phần tử ở phía bên phải của phần tử mid. Điều này được thực hiện bằng cách đặt low = mid + 1.
Bước 6: Mặt khác, so sánh x với phần tử ở giữa của các phần tử ở bên trái của phần tử mid. Điều này được thực hiện bằng cách thiết lập high = mid – 1.
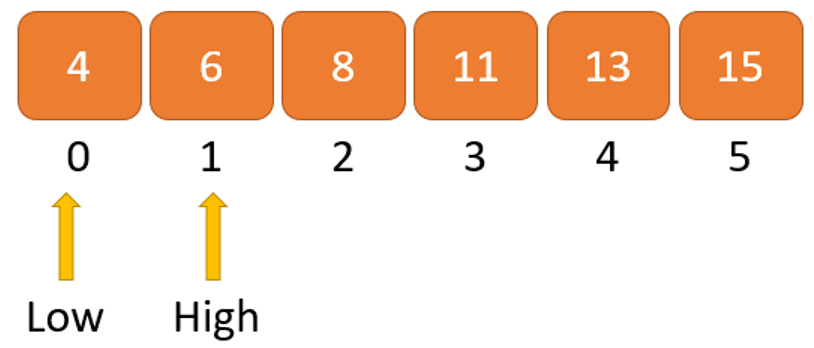
Bước 7: Lặp lại từ bước 3 đến bước 6 cho đến khi low = high.
Bước 8: Và cuối cùng ta sẽ tìm được phần tử cần tìm là 6.
Viết chương trình tìm kiếm nhị phân với ngôn ngữ C
1. Phương pháp sử dụng vòng lặp
Thực hiện cho đến khi các con trỏ low trỏ cùng vị trí của con trỏ high. mid = (low + high) / 2 Nếu x == arr[mid] Trả về mid Nếu x > arr[mid] // x ở phía bên phải low = mid + 1 Nếu không // x ở bên trái high = mid – 1
2. Phương thức sử dụng kỹ thuật đệ quy
Hàm tìm kiếm nhị phân(arr, x, low, high) Nếu low > high Trả về False Nếu không mid = (low + high) / 2 Nếu x = arr[mid] Trả về mid Nếu x < arr[mid] Trả về hàm tìm kiếm nhị phân(arr, x, mid + 1, high) Nếu không Trả về hàm tìm kiếm nhị phân (arr, x, low, mid - 1)
Ví dụ: Triển khai tìm kiếm nhị phân bằng ngôn ngữ lập trình C.
#include <stdio.h>
int search(int arr[], int x, int low, int high) {
while (low <= high) {
int mid = low + (high - low) / 2;
if (arr[mid] == x)
return mid;
if (arr[mid] < x)
low = mid + 1;
else
high = mid - 1;
}
return -1;
}
int main(void) {
int arr[] = {4, 6, 8, 11, 13, 15};
int n = sizeof(arr) / sizeof(arr[0]);
int x = 6;
int kq = search(arr, x, 0, n - 1);
if (kq == -1)
printf("Không tìm thấy");
else
printf("Phần tử cần tìm nằm ở vị trí %d", kq);
return 0;
}
Kết quả:
Phần tử cần tìm nằm ở vị trí 1
Ví dụ 2:
#include <stdio.h>
int search(int arr[], int find, int low, int high) {
if (high >= low) {
int mid = low + (high - low) / 2;
if (arr[mid] == find)
return mid;
if (arr[mid] > find)
return search(arr, find, low, mid - 1);
return search(arr, find, mid + 1, high);
}
return -1;
}
int main(void) {
int arr[] = {4, 6, 8, 11, 13, 15};
int n = sizeof(arr) / sizeof(arr[0]);
int find = 6;
int kq = search(arr, find, 0, n - 1);
if (kq == -1)
printf("Không tìm thấy");
else
printf("Phần tử nằm tại vị trí %d", kq);
}
Kết quả:
Phần tử nằm tại vị trí 1
Thuật toán tìm kiếm tuyến tính (Linear Search)
Khái niệm
Tìm kiếm tuyến tính (Linear Search) hay còn gọi là thuật toán tìm kiếm tuần tự (Sequetial Search) là thuật toán tìm kiếm đơn giản nhất để tìm kiếm một phần tử trong danh sách theo thứ tự tuần tự. Chúng ta sẽ bắt đầu từ một đầu và kiểm tra mọi phần tử cho đến khi phần tử cần tìm không được tìm thấy.
Ý tưởng bài toán
Thuật toán tìm kiêm tuyến tính là một thuật toán khá đơn giản. Sau đây là ý tưởng triển khai thuật toán.
- Bắt đầu từ bản ghi đầu tiên của mảng, duyệt từ đầu mảng đến cuối mảng với x.
- Nếu phần tử đang duyệt bằng x thì trả về vị trí.
- Nếu không tìm thấy bất cứ phần từ nào khi đã duyệt hết thì trả về -1.
Cách thức hoạt động của thuật toán Linear Search
Bắt đầu từ phần tử ngoài cùng bên trái của mảng và lần lượt so sánh phần tử chúng ta đang tìm kiếm với từng phần tử của mảng.
Nếu có sự trùng khớp giữa phần tử chúng ta đang tìm kiếm và một phần tử của mảng, ta sẽ trả về chỉ số của phần tử đó.
Nếu không có kết quả phù hợp nào giữa phần tử chúng ta đang tìm kiếm và một phần tử của mảng, trả về giá trị là -1 hoặc bất kỳ giá trị nào mà không nằm trong chỉ số của danh sách.
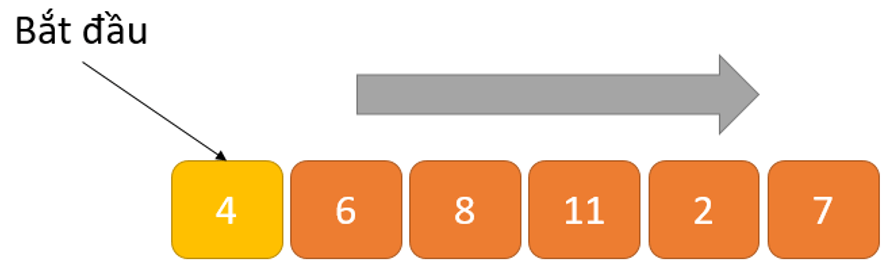
Ví dụ, các bước sau được thực hiện để tìm kiếm phần tử k = 2 trong danh sách dưới đây.
Giả sử ta có mảng như sau:
Bắt đầu từ phần tử đầu tiên, so sánh k với mỗi phần tử x.
Nếu x == k, ta sẽ trả về chỉ số của phần tử đó.
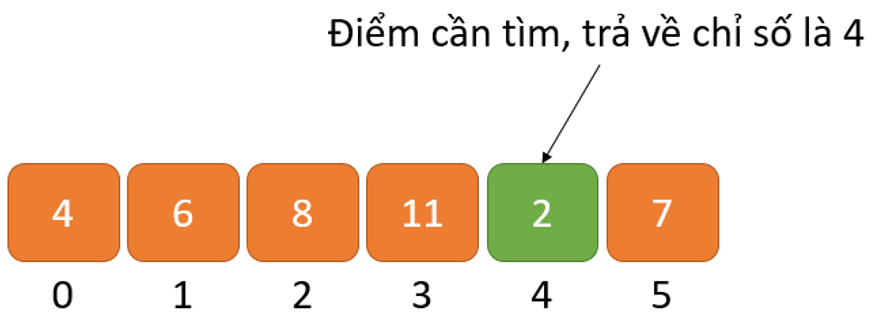
Nếu không, trả về thông báo là không tìm thấy phần tử trong danh sách. Trong mảng trên, giá trị k cần tìm có chỉ số là 4 trong mảng.
Viết chương trình thuật toán tìm kiếm tuyến tính với ngôn ngữ C
Hàm tìm kiếm tuyến tính
Sử dụng vòng lặp for để duyệt qua từng phần tử trong danh sách/ tập hợp
Nếu giá trị của phần tử bằng giá trị cần tìm
Trả về chỉ số của phần tử đó trong danh sách/ tập hợp
Ví dụ: Triển khai thuật toán tìm kiếm phần tử trong mảng bằng ngôn ngữ lập trình C.
#include <stdio.h>
int linear_search(int arr[], int n, int find) {
for (int i = 0; i < n; i++)
if (arr[i] == find)
return i;
return -1;
}
int main() {
int arr[] = {4, 6, 8, 11, 2, 7};
int x = 2;
int n = sizeof(arr) / sizeof(arr[0]);
int kq = linear_search(arr, n, x);
(kq == -1) ? printf("Không tìm thấy") : printf("Giá trị cần tìm nằm tại vị trí: %d", kq);
}
Kết quả:
Giá trị cần tìm nằm tại vị trí: 4
Bài tập vận dụng
Thuật toán tìm kiếm nội suy (Interpolation Search)
Khái niệm
Tìm kiếm nội suy hay Interpolation Search là một loại thuật toán hay giải thuật tìm kiếm. Tìm kiếm nội suy là một thuật toán cải tiến hơn so với tìm kiếm nhị phân cho các trường hợp, trong đó các giá trị trong một mảng đã được sắp xếp được phân phối đồng đều.
Tìm kiếm nhị phân sẽ chuyển đến phần tử giữa để kiểm tra, và loại bỏ các phần tử còn lại tùy thuộc vào giá trị tìm kiếm và giá trị của phần tử nằm ở giữa. Mặt khác, giải thuật tìm kiếm nội suy có thể đi đến các vị trí khác nhau tùy theo giá trị của khóa đang được tìm kiếm. Tại mỗi bước tìm kiếm, tìm kiếm nội suy sẽ tính toán vùng không gian mà phần tử cần tìm có thể xuất hiện, dựa trên giá trị Low và High của không gian tìm kiếm.
Ví dụ, nếu giá trị của khóa gần với phần tử cuối cùng, tìm kiếm nội suy có khả năng sẽ có xu hướng bắt đầu quá trình tìm kiếm ở phía cuối.
Tìm kiếm nội suy sử dụng công thức sau đây để tìm kiếm vị trí ở giữa, trong đó arr[low] và arr[high] là vùng không gian tìm kiếm và x là phần tử cần tìm.
Mid = low + ((x-arr[low])*(high-low)/(arr[high] – arr[low]));
Các bước về cách hoạt động của giải thuật tìm kiếm nội suy:
- Trong một vòng lặp, ta sẽ tính giá trị của Mid bằng công thức bên trên.
- Nếu có sự trùng khớp, ta trả về chỉ số của phần tử và kết thúc việc tìm kiếm.
- Nếu phần tử nhỏ hơn arr[mid], ta sẽ tính toán vị trí thăm dò của mảng con bên trái. Nếu không, ta sẽ thực hiện quá trình tính toán tương tự trong mảng con bên phải.
- Lặp lại cho đến khi tìm thấy kết quả phù hợp hoặc mảng con giảm xuống 0.
Ý tưởng bài toán
Tìm kiếm từ đầu cho đến cuối mảng (hoặc ngược lại).
- Nếu tìm thấy trả vị trí của kết quả tìm kiếm.
- Nếu không tìm thấy thì trả về 1.
Viết chương trình tìm kiếm nội suy với C
Sau đây là một ví dụ về cách viết cho giải thuật tìm kiếm nội suy dựa trên các bước ta đã cung cấp.
Ví dụ: Triển khai tìm kiếm nội suy bằng ngôn ngữ lập trình C.
#include <stdio.h>
int search(int arr[], int n, int find)
{
int low = 0, high = n - 1, mid;
while (arr[high] != arr[low] && find >= arr[low] && find <= arr[high])
{
mid = low + ((find - arr[low]) * (high - low) / (arr[high] - arr[low]));
if (find == arr[mid]) {
return mid;
}
else if (find < arr[mid]) {
high = mid - 1;
}
else {
low = mid + 1;
}
}
if (find == arr[low]) {
return low;
}
else {
return -1;
}
}
int main(void)
{
int arr[] = {4, 6, 8, 11, 13, 15};
int value_to_find = 6;
int n = sizeof(arr)/sizeof(arr[0]);
int pos = search(arr, n, value_to_find);
if (pos != -1) {
printf("Phần tử cần tìm nằm ở vị trí %d", pos);
} else {
printf("Không tìm thấy");
}
return 0;
}
Kết quả:
Phần tử cần tìm nằm ở vị trí 1
Thuật toán tìm kiếm nhảy (Jump Search)
Trong khoa học máy tính , tìm kiếm nhảy hoặc tìm kiếm khối (jump search hoặc block search) đề cập đến thuật toán tìm kiếm cho danh sách đẫ được sắp xếp. Ý tưởng cơ bản là kiểm tra ít yếu tố hơn ( tìm kiếm tuyến tính ) bằng cách nhảy về phía trước bằng các bước cố định hoặc bỏ qua một số yếu tố thay vì tìm kiếm tất cả các yếu tố.
Nguyên lý cơ bản của Jump Search
Cũng giống như giải thuật Binary Search. Jump Search cũng yêu cầu danh sách đã cho phải là một danh sách đã được sắp xếp theo thứ tự đã biết.
Ví dụ là tăng dần.
Cơ chế của Jump Search đó là tìm ra một hệ số nhảy được tính bằng : Căn bậc hai của số phần tử.
Từ hệ số tìm được, Jump Search sẽ thực hiện nhảy phần tử theo hệ số để tìm ra phần từ lớn hơn giá trị tìm kiếm.
=> Phần tử tìm kiếm sẽ nằm trong khoảng của nhảy mà chứa phần từ lớn hơn giá trị tìm kiếm ở trên.
Minh Họa hình vẽ như sau:
Tôi có tập 9 phần từ đã được sắp xếp theo thứ tự tăng dần.
Tôi xác định giá trị nhảy là step = √9 = 3 .
Giả sử giá trị cần tìm là 33.
Sử dụng một biến prev để lưu vị trí bắt đầu.
Một biến jump để nhảy.
Step 1:
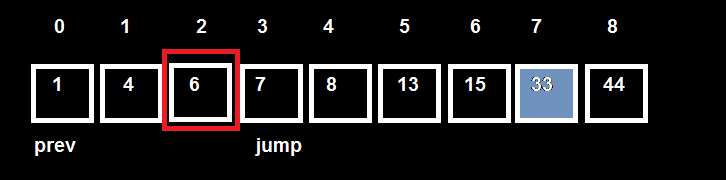
Prev = 0, jump =step = 3
Kiểm tra T[jump – 1] => T[2] = 6 < 33 =>Nhảy step 2.
Step 2:
Gán prev = jump = 3.
Nhảy jum theo step => jum = jump + step = 6
Tiếp tục kiểm tra T[jum -1] => T[5] = 13 < 33 => Nhảy step 3
Step 3:
Gán prev = jump = 6
Nhảy jump = jump + step = 9 (bằng số phần tử, nếu jum lớn hơn n thì gán jum = n)
Lại kiểm tra T[jump – 1] => T[8] = 44 > 33 => Đã tìm được khoảng chứa giá trị cần tìm.
Khoảng chứa giá trị cần tìm là từ prev = 6 , jump = 9.
Lúc này chúng ta chỉ việc kiểm tra tuyến tính tệp từ vị trí prev đến jump để tìm ra giá trị cần tìm.
Sử dụng for hoặc while để duyệt phần tử trong khoảng prev – jump.
Giải thuật tìm kiếm nhảy Jump Search
Giải thuật tìm kiếm nhảy
Input: Cho một danh sách đã sắp xếp L, chiều dài n và khóa là s.
Output: Vị trí của s trong L, hoặc trả về null khi s không nằm trong L.
a ← 0
b ← ⌊√n⌋
while Lmin(b,n)-1 < s do
a ← b
b ← b + ⌊√n⌋
if a ≥ n then
return nothing
while La < s do
a ← a + 1
if a = min(b,n)
return nothing
if La = s then
return a
else
return nothing
Viết chương trình tìm kiếm nội suy với C
Hãy xem xét các mảng sau: A[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610]. Độ dài của mảng là 16. Sử dụng thuật toán tìm kiếm nhảy để tìm giá trị 55 với bước nhảy là 4 được thực hiện như sau:
BƯỚC 1: Nhảy từ chỉ số 0 sang chỉ số 4;
BƯỚC 2: Chuyển từ chỉ số index 4 sang chỉ số index 8;
BƯỚC 3: Chuyển từ chỉ số index 8 sang chỉ số index 12;
BƯỚC 4: Vì phần tử ở chỉ số index 12 lớn hơn 55, bạn sẽ phải quay lại một bước để đến với chỉ mục index 9.
BƯỚC 5: Thực hiện tìm kiếm tuyến tính từ chỉ mục 9 để lấy phần tử 55.
Kích thước khối tối ưu được bỏ qua trong tìm kiếm nhảy là gì?
Trong trường hợp xấu nhất, chúng tôi phải thực hiện các bước nhảy n/m và nếu giá trị được kiểm tra cuối cùng lớn hơn phần tử cần tìm, ta phải thực hiện so sánh m-1 nhiều hơn cho tìm kiếm tuyến tính. Do đó, tổng số so sánh trong trường hợp xấu nhất sẽ là ((n / m) + m – 1). Giá trị của hàm ((n / m) + m – 1) sẽ tối thiểu khi m = √n. Do đó, kích thước bước nhảy tốt nhất là m = n .
Điểm quan trọng
- Chỉ hoạt động với các mảng được sắp xếp.
- Kích thước tối ưu của một khối được nhảy là (√ n). Điều này làm cho độ phức tạp về thời gian của Jump Search là O (√ n).
- Độ phức tạp về thời gian của Tìm kiếm nhảy là giữa Tìm kiếm tuyến tính ((O (n)) và Tìm kiếm nhị phân (O (Log n)).
- Tìm kiếm Nhị phân tốt hơn Tìm kiếm Nhảy, nhưng Tìm kiếm Nhảy có một ưu điểm là chúng ta chỉ duyệt lại một lần (Tìm kiếm Nhị phân có thể yêu cầu tối đa O (Nhật ký n) bước nhảy, hãy xem xét tình huống trong đó phần tử cần tìm là phần tử nhỏ nhất hoặc nhỏ hơn nhỏ nhất). Vì vậy, trong một hệ thống mà tìm kiếm nhị phân rất tốn kém, chúng tôi sử dụng Jump Search.
Kết
Hi vọng sau bài viết này các bạn đã hiểu những kiến thức cơ bản về thuật toán tìm kiếm và thực hành chúng trên ngôn ngữ C.
Nếu bạn thấy bài viết này có ích hãy để lại bình luận và đừng quên ra nhập Hội Anh Em Nghiện Lập trình nhé.
